Ruby Hacking Guide
Translated by Clifford Escobar CAOILE
Chapter 3: Names and Name Table
`st_table`
`st_table` has already appeared several times as a method table and an instance table. In this chapter let’s look at the structure of the `st_table` in detail.
Summary
I previously mentioned that the `st_table` is a hash table. What is a hash table? It is a data structure that records one-to-one relations, for example, a variable name and its value, or a function name and its body, etc.
However, data structures other than hash tables can, of course, record one-to-one relations. For example, a list of the following structs will suffice for this purpose.
struct entry {
ID key;
VALUE val;
struct entry *next; /* point to the next entry */
};
However, this method is slow. If the list contains a thousand items, in the worst case, it is necessary to traverse a thousand links. In other words, the search time increases in proportion to the number of elements. This is bad. Since ancient times, various speed improvement methods have been conceived. The hash table is one of those improved methods. In other words, the point is not that the hash table is necessary but that it can be made faster.
Now then, let us examine the `st_table`. As it turns out, this library is not created by Matsumoto, rather:
▼ `st.c` credits
1 /* This is a public domain general purpose hash table package
written by Peter Moore @ UCB. */
(st.c)
as shown above.
By the way, when I searched Google and found another version, it mentioned that `st_table` is a contraction of “STring TABLE”. However, I find it contradictory that it has both “general purpose” and “string” aspects.
What is a hash table?
A hash table can be thought as the following: Let us think of an array with `n` items. For example, let us make `n`=64 (figure 1).

Then let us specify a function `f` that takes a key and produces an integer `i` from 0 to `n`-1 (0-63). We call this `f` a hash function. `f` when given the same key always produces the same `i`. For example, if we can assume that the key is limited to positive integers, when the key is divided by 64, the remainder should always fall between 0 and 63. Therefore, this calculating expression has a possibility of being the function `f`.
When recording relationships, given a key, function `f` generates `i`, and places the value into index `i` of the array we have prepared. Index access into an array is very fast. The key concern is changing a key into an integer.
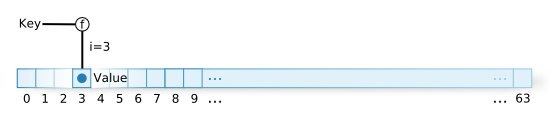
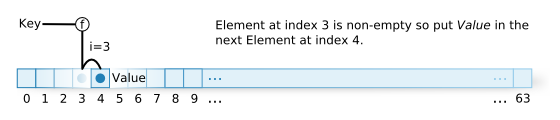
However, in the real world it isn’t that easy. There is a critical problem with this idea. Because `n` is only 64, if there are more than 64 relationships to be recorded, it is certain that there will be the same index for two different keys. It is also possible that with fewer than 64, the same thing can occur. For example, given the previous hash function “key % 64”, keys 65 and 129 will both have a hash value of 1. This is called a hash value collision. There are many ways to resolve such a collision.
One solution is to insert into the next element when a collision occurs. This is called open addressing. (Figure 3).
Other than using the array like this, there are other possible approaches, like using a pointer to a respective linked list in each element of the array. Then when a collision occurs, grow the linked list. This is called chaining. (Figure 4) `st_table` uses this chaining method.

However, if it can be determined a priori what set of keys will be used, it is possible to imagine a hash function that will never create collisions. This type of function is called a “perfect hash function”. Actually, there are tools which create a perfect hash function given a set of arbitrary strings. GNU gperf is one of those. `ruby`‘s parser implementation uses GNU gperf but… this is not the time to discuss it. We’ll discuss this in the second part of the book.
Data Structure
Let us start looking at the source code. As written in the introductory chapter, if there is data and code, it is better to read the data first. The following is the data type of `st_table`.
▼ `st_table`
9 typedef struct st_table st_table;
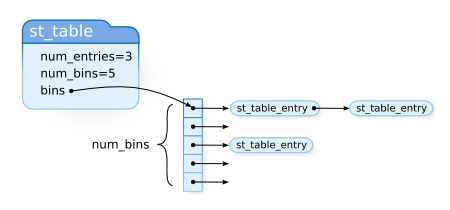
16 struct st_table {
17 struct st_hash_type *type;
18 int num_bins; /* slot count */
19 int num_entries; /* total number of entries */
20 struct st_table_entry **bins; /* slot */
21 };
(st.h)
▼ `struct st_table_entry`
16 struct st_table_entry {
17 unsigned int hash;
18 char *key;
19 char *record;
20 st_table_entry *next;
21 };
(st.c)
`st_table` is the main table structure. `st_table_entry` is a holder that stores one value. `st_table_entry` contains a member called `next` which of course is used to make `st_table_entry` into a linked list. This is the chain part of the chaining method. The `st_hash_type` data type is used, but I will explain this later. First let me explain the other parts so you can compare and understand the roles.
So, let us comment on `st_hash_type`.
▼ `struct st_hash_type`
11 struct st_hash_type {
12 int (*compare)(); /* comparison function */
13 int (*hash)(); /* hash function */
14 };
(st.h)
This is still Chapter 3 so let us examine it attentively.
int (*compare)()
This part shows, of course, the member `compare` which has a data type of “a pointer to a function that returns an `int`”. `hash` is also of the same type. This variable is substituted in the following way:
int
great_function(int n)
{
/* ToDo: Do something great! */
return n;
}
{
int (*f)();
f = great_function;
And it is called like this:
(*f)(7);
}
Here let us return to the `st_hash_type` commentary. Of the two members `hash` and `compare`, `hash` is the hash function `f` explained previously.
On the other hand, `compare` is a function that evaluates if the key is actually the same or not. With the chaining method, in the spot with the same hash value `n`, multiple elements can be inserted. To know exactly which element is being searched for, this time it is necessary to use a comparison function that we can absolutely trust. `compare` will be that function.
This `st_hash_type` is a good generalized technique. The hash table itself cannot determine what the stored keys’ data type will be. For example, in `ruby`, `st_table`’s keys are `ID` or `char*` or `VALUE`, but to write the same kind of hash for each (data type) is foolish. Usually, the things that change with the different key data types are things like the hash function. For things like memory allocation and collision detection, typically most of the code is the same. Only the parts where the implementation changes with a differing data type will be bundled up into a function, and a pointer to that function will be used. In this fashion, the majority of the code that makes up the hash table implementation can use it.
In object-oriented languages, in the first place, you can attach a procedure to an object and pass it (around), so this mechanism is not necessary. Perhaps it more correct to say that this mechanism is built-in as a language’s feature.
`st_hash_type` example
The usage of a data structure like `st_hash_type` is good as an abstraction. On the other hand, what kind of code it actually passes through may be difficult to understand. If we do not examine what sort of function is used for `hash` or `compare`, we will not grasp the reality. To understand this, it is probably sufficient to look at `st_init_numtable()` introduced in the previous chapter. This function creates a table for integer data type keys.
▼ `st_init_numtable()`
182 st_table*
183 st_init_numtable()
184 {
185 return st_init_table(&type_numhash);
186 }
(st.c)
`st_init_table()` is the function that allocates the table memory and so on. `type_numhash` is an `st_hash_type` (it is the member named “type” of `st_table`). Regarding this `type_numhash`:
▼ `type_numhash`
37 static struct st_hash_type type_numhash = {
38 numcmp,
39 numhash,
40 };
552 static int
553 numcmp(x, y)
554 long x, y;
555 {
556 return x != y;
557 }
559 static int
560 numhash(n)
561 long n;
562 {
563 return n;
564 }
(st.c)
Very simple. The table that the `ruby` interpreter uses is by and large this `type_numhash`.
`st_lookup()`
Now then, let us look at the function that uses this data structure. First, it’s a good idea to look at the function that does the searching. Shown below is the function that searches the hash table, `st_lookup()`.
▼ `st_lookup()`
247 int
248 st_lookup(table, key, value)
249 st_table *table;
250 register char *key;
251 char **value;
252 {
253 unsigned int hash_val, bin_pos;
254 register st_table_entry *ptr;
255
256 hash_val = do_hash(key, table);
257 FIND_ENTRY(table, ptr, hash_val, bin_pos);
258
259 if (ptr == 0) {
260 return 0;
261 }
262 else {
263 if (value != 0) *value = ptr->record;
264 return 1;
265 }
266 }
(st.c)
The important parts are pretty much in `do_hash()` and `FIND_ENTRY()`. Let us look at them in order.
▼ `do_hash()`
68 #define do_hash(key,table) (unsigned int)(*(table)->type->hash)((key)) (st.c)
Just in case, let us write down the macro body that is difficult to understand:
(table)->type->hash
is a function pointer where the `key` is passed as a parameter. This is the syntax for calling the function. `*` is not applied to `table`. In other words, this macro is a hash value generator for a `key`, using the prepared hash function `type→hash` for each data type.
Next, let us examine `FIND_ENTRY()`.
▼ `FIND_ENTRY()`
235 #define FIND_ENTRY(table, ptr, hash_val, bin_pos) do {\
236 bin_pos = hash_val%(table)->num_bins;\
237 ptr = (table)->bins[bin_pos];\
238 if (PTR_NOT_EQUAL(table, ptr, hash_val, key)) {\
239 COLLISION;\
240 while (PTR_NOT_EQUAL(table, ptr->next, hash_val, key)) {\
241 ptr = ptr->next;\
242 }\
243 ptr = ptr->next;\
244 }\
245 } while (0)
227 #define PTR_NOT_EQUAL(table, ptr, hash_val, key) ((ptr) != 0 && \
(ptr->hash != (hash_val) || !EQUAL((table), (key), (ptr)->key)))
66 #define EQUAL(table,x,y) \
((x)==(y) || (*table->type->compare)((x),(y)) == 0)
(st.c)
`COLLISION` is a debug macro so we will (should) ignore it.
The parameters of `FIND_ENTRY()`, starting from the left are:
- `st_table`
- the found entry will be pointed to by this parameter
- hash value
- temporary variable
And, the second parameter will point to the found `st_table_entry*`.
At the outermost level, a `do` .. `while(0)` is used to safely wrap up a multiple expression macro. This is `ruby`‘s, or rather, C language’s preprocessor idiom. In the case of `if(1)`, there may be a danger of adding an `else` part. In the case of `while(1)`, it becomes necessary to add a `break` at the very end.
Also, there is no semicolon added after the `while(0)`.
FIND_ENTRY();
This is so that the semicolon that is normally written at the end of an expression will not go to waste.
`st_add_direct()`
Continuing on, let us examine `st_add_direct()` which is a function that adds a new relationship to the hash table. This function does not check if the key is already registered. It always adds a new entry. This is the meaning of `direct` in the function name.
▼ `st_add_direct()`
308 void
309 st_add_direct(table, key, value)
310 st_table *table;
311 char *key;
312 char *value;
313 {
314 unsigned int hash_val, bin_pos;
315
316 hash_val = do_hash(key, table);
317 bin_pos = hash_val % table->num_bins;
318 ADD_DIRECT(table, key, value, hash_val, bin_pos);
319 }
(st.c)
Just as before, the `do_hash()` macro that obtains a value is called here. After that, the next calculation is the same as at the start of `FIND_ENTRY()`, which is to exchange the hash value for a real index.
Then the insertion operation seems to be implemented by `ADD_DIRECT()`. Since the name is all uppercase, we can anticipate that is a macro.
▼ `ADD_DIRECT()`
268 #define ADD_DIRECT(table, key, value, hash_val, bin_pos) \
269 do { \
270 st_table_entry *entry; \
271 if (table->num_entries / (table->num_bins) \
> ST_DEFAULT_MAX_DENSITY) { \
272 rehash(table); \
273 bin_pos = hash_val % table->num_bins; \
274 } \
275 \
/* (A) */ \
276 entry = alloc(st_table_entry); \
277 \
278 entry->hash = hash_val; \
279 entry->key = key; \
280 entry->record = value; \
/* (B) */ \
281 entry->next = table->bins[bin_pos]; \
282 table->bins[bin_pos] = entry; \
283 table->num_entries++; \
284 } while (0)
(st.c)
The first `if` is an exception case so I will explain it afterwards.
(A) Allocate and initialize a `st_table_entry`.
(B) Insert the `entry` into the start of the list. This is the idiom for handling the list. In other words,
entry->next = list_beg; list_beg = entry;
makes it possible to insert an entry to the front of the list. This is similar to “cons-ing” in the Lisp language. Check for yourself that even if `list_beg` is NULL, this code holds true.
Now, let me explain the code I left aside.
▼ `ADD_DIRECT()`-`rehash`
271 if (table->num_entries / (table->num_bins) \
> ST_DEFAULT_MAX_DENSITY) { \
272 rehash(table); \
273 bin_pos = hash_val % table->num_bins; \
274 } \
(st.c)
`DENSITY` is “concentration”. In other words, this conditional checks if the hash table is “crowded” or not. In the `st_table`, as the number of values that use the same `bin_pos` increases, the longer the link list becomes. In other words, search becomes slower. That is why for a given `bin` count, when the average elements per bin become too many, `bin` is increased and the crowding is reduced.
The current `ST_DEFAULT_MAX_DENSITY` is
▼ `ST_DEFAULT_MAX_DENSITY`
23 #define ST_DEFAULT_MAX_DENSITY 5 (st.c)
Because of this setting, if in all `bin_pos` there are 5 `st_table_entries`, then the size will be increased.
`st_insert()`
`st_insert()` is nothing more than a combination of `st_add_direct()` and `st_lookup()`, so if you understand those two, this will be easy.
▼ `st_insert()`
286 int
287 st_insert(table, key, value)
288 register st_table *table;
289 register char *key;
290 char *value;
291 {
292 unsigned int hash_val, bin_pos;
293 register st_table_entry *ptr;
294
295 hash_val = do_hash(key, table);
296 FIND_ENTRY(table, ptr, hash_val, bin_pos);
297
298 if (ptr == 0) {
299 ADD_DIRECT(table, key, value, hash_val, bin_pos);
300 return 0;
301 }
302 else {
303 ptr->record = value;
304 return 1;
305 }
306 }
(st.c)
It checks if the element is already registered in the table. Only when it is not registered will it be added. If there is a insertion, return 0. If there is no insertion, return a 1.
`ID` and Symbols
I’ve already discussed what an `ID` is. It is a correspondence between an arbitrary string of characters and a value. It is used to declare various names. The actual data type is `unsigned int`.
From `char*` to `ID`
The conversion from string to `ID` is executed by `rb_intern()`. This function is rather long, so let’s omit the middle.
▼ `rb_intern()` (simplified)
5451 static st_table *sym_tbl; /* char* to ID */
5452 static st_table *sym_rev_tbl; /* ID to char* */
5469 ID
5470 rb_intern(name)
5471 const char *name;
5472 {
5473 const char *m = name;
5474 ID id;
5475 int last;
5476
/* If for a name, there is a corresponding ID that is already
registered, then return that ID */
5477 if (st_lookup(sym_tbl, name, &id))
5478 return id;
/* omitted ... create a new ID */
/* register the name and ID relation */
5538 id_regist:
5539 name = strdup(name);
5540 st_add_direct(sym_tbl, name, id);
5541 st_add_direct(sym_rev_tbl, id, name);
5542 return id;
5543 }
(parse.y)
The string and `ID` correspondence relationship can be accomplished by using the `st_table`. There probably isn’t any especially difficult part here.
What is the omitted section doing? It is treating global variable names and instance variables names as special and flagging them. This is because in the parser, it is necessary to know the variable’s classification from the `ID`. However, the fundamental part of `ID` is unrelated to this, so I won’t explain it here.
From `ID` to `char*`
The reverse of `rb_intern()` is `rb_id2name()`, which takes an `ID` and generates a `char*`. You probably know this, but the 2 in `id2name` is “to”. “To” and “two” have the same pronounciation, so “2” is used for “to”. This syntax is often seen.
This function also sets the `ID` classification flags so it is long. Let me simplify it.
▼ `rb_id2name()` (simplified)
char *
rb_id2name(id)
ID id;
{
char *name;
if (st_lookup(sym_rev_tbl, id, &name))
return name;
return 0;
}
Maybe it seems that it is a little over-simplified, but in reality if we remove the details it really becomes this simple.
The point I want to emphasize is that the found `name` is not copied. The `ruby` API does not require (or rather, it forbids) the `free()`-ing of the return value. Also, when parameters are passed, it always copies them. In other words, the creation and release is completed by one side, either by the user or by `ruby`.
So then, when creation and release cannot be accomplished (when passed it is not returned) on a value, then a Ruby object is used. I have not yet discussed it, but a Ruby object is automatically released when it is no longer needed, even if we are not taking care of the object.
Converting `VALUE` and `ID`
`ID` is shown as an instance of the `Symbol` class at the Ruby level. And it can be obtained like so: `“string”.intern`. The implementation of `String#intern` is `rb_str_intern()`.
▼ `rb_str_intern()`
2996 static VALUE
2997 rb_str_intern(str)
2998 VALUE str;
2999 {
3000 ID id;
3001
3002 if (!RSTRING(str)->ptr || RSTRING(str)->len == 0) {
3003 rb_raise(rb_eArgError, "interning empty string");
3004 }
3005 if (strlen(RSTRING(str)->ptr) != RSTRING(str)->len)
3006 rb_raise(rb_eArgError, "string contains `\\0'");
3007 id = rb_intern(RSTRING(str)->ptr);
3008 return ID2SYM(id);
3009 }
(string.c)
This function is quite reasonable as a `ruby` class library code example. Please pay attention to the part where `RSTRING()` is used and casted, and where the data structure’s member is accessed.
Let’s read the code. First, `rb_raise()` is merely error handling so we ignore it for now. The `rb_intern()` we previously examined is here, and also ID2SYM is here. `ID2SYM()` is a macro that converts `ID` to `Symbol`.
And the reverse operation is accomplished using `Symbol#to_s` and such. The implementation is in `sym_to_s`.
▼ `sym_to_s()`
522 static VALUE
523 sym_to_s(sym)
524 VALUE sym;
525 {
526 return rb_str_new2(rb_id2name(SYM2ID(sym)));
527 }
(object.c)
`SYM2ID to an `ID`.
It looks like the function is not doing anything unreasonable. However, it is probably necessary to pay attention to the area around the memory handling. `rb_id2name()` returns a `char*` that must not be `free()`. `rb_str_new2()` copies the parameter’s `char*` and uses the copy (and does not change the parameter). In this way the policy is consistent, which allows the line to be written just by chaining the functions.